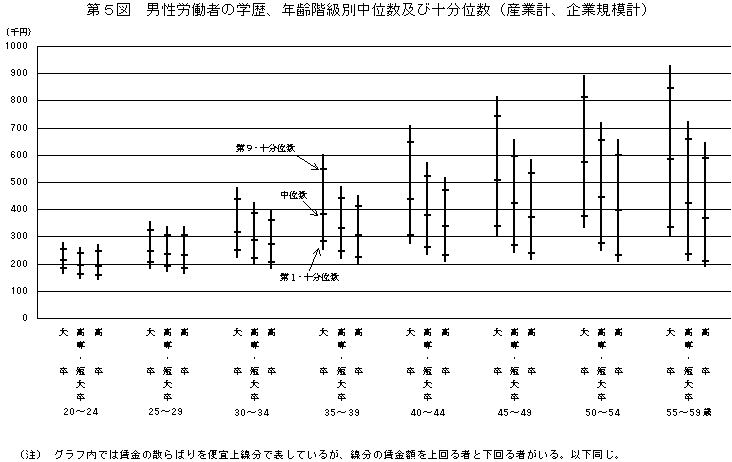
○中 位 数 ‥‥ 二等分した節の者の賃金
○第9・十分位数 ‥‥ 十等分し、高い方から最初の節の者の賃金

その値が小さいほど分布の広がりの程度が小さいことを示す。
| ◯十分位分散係数= | 第9・十分位数 − 第1・十分位数 |
| 2 × 中位数 |
第12表 男性労働者の学歴、年齢階級別特性値
(産業計、企業規模計)
| 年齢階級 (歳) |
大 卒 | 高専・短大卒 | 高 卒 | ||||||||||||
| 第1・十分位数 | 中位数 | 第9・十分位数 | 分位数間の差 | 十分位分散係数 | 第1・十分位数 | 中位数 | 第9・十分位数 | 分位数間の差 | 十分位分散係数 | 第1・十分位数 | 中位数 | 第9・十分位数 | 分位数間の差 | 十分位分散係数 | |
| (千円) | (千円) | (千円) | (千円) | (千円) | (千円) | (千円) | (千円) | (千円) | (千円) | (千円) | (千円) | ||||
| 計 | 219.1 | 353.4 | 641.8 | 422.7 | 0.60 | 182.9 | 268.6 | 463.4 | 280.5 | 0.52 | 182.1 | 289.1 | 479.7 | 297.6 | 0.51 |
| 20〜24 | 184.7 | 211.7 | 253.2 | 68.5 | 0.16 | 162.5 | 193.1 | 238.7 | 76.2 | 0.20 | 159.5 | 192.4 | 246.8 | 87.3 | 0.23 |
| 25〜29 | 204.9 | 247.4 | 323.2 | 118.3 | 0.24 | 190.0 | 233.6 | 306.0 | 116.0 | 0.25 | 183.3 | 230.5 | 306.4 | 123.1 | 0.27 |
| 30〜34 | 249.0 | 314.5 | 438.6 | 189.6 | 0.30 | 222.2 | 288.3 | 386.5 | 164.3 | 0.28 | 205.9 | 271.0 | 360.0 | 154.1 | 0.28 |
| 35〜39 | 282.6 | 381.4 | 549.2 | 266.6 | 0.35 | 246.5 | 330.3 | 441.5 | 195.0 | 0.30 | 222.6 | 305.4 | 411.9 | 189.3 | 0.31 |
| 40〜44 | 306.0 | 437.3 | 646.5 | 340.5 | 0.39 | 261.7 | 377.9 | 522.0 | 260.3 | 0.34 | 231.4 | 338.0 | 472.2 | 240.8 | 0.36 |
| 45〜49 | 338.6 | 507.0 | 741.4 | 402.8 | 0.40 | 269.5 | 421.2 | 596.9 | 327.4 | 0.39 | 239.6 | 372.4 | 531.8 | 292.2 | 0.39 |
| 50〜54 | 373.5 | 572.0 | 811.7 | 438.2 | 0.38 | 276.4 | 444.1 | 655.9 | 379.5 | 0.43 | 233.4 | 395.7 | 597.7 | 364.3 | 0.46 |
| 55〜59 | 334.9 | 583.1 | 845.6 | 510.7 | 0.44 | 236.9 | 421.6 | 658.4 | 421.5 | 0.50 | 211.3 | 367.8 | 589.8 | 378.5 | 0.51 |
| (注)1) | 分位数とは、具体的には、全労働者を賃金の低い者から高い者へと一列に並べて、全労働者の所定の何等分目かに位置する者の値である。図解すると次のとおりである。 | |||||
| ○第1・十分位数 ‥‥
十等分し、低い方から最初の節の者の賃金 ○中 位 数 ‥‥ 二等分した節の者の賃金 ○第9・十分位数 ‥‥ 十等分し、高い方から最初の節の者の賃金 |
 |
|||||
| 2) | ここでいう分位数間の差とは、第9・十分位数から第1・十分位数を引いたものである。 | |||||
| 3) | 十分位分散係数とは、次の算式により計算された数値をいう。 その値が小さいほど分布の広がりの程度が小さいことを示す。
|
|||||